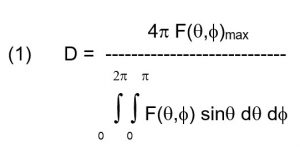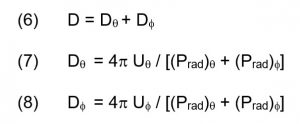הכיווניות של אנטנה
ההגדרה הראשונית של כיווניות אנטנה antenna directivityניתנת על ידי היחס בין הערך המכסימלי של עקום הקרינה הדו ממדי F(q,f) לבין הערך הממוצע של עקום הקרינה על פני המרחב כולו. הערך הממוצע ניתן על ידי סכימה על כדור וחלוקה בזווית המרחבית 4p כמתואר בנוסחה הבאה [1] – [5] :
בהינתן אנטנה המפזרת את מירב הקרינה שלה אל זווית מרחבית Wa משתמשים בקירוב הנקרא על שם Kraus לפי:
כאשר p4 היא הזווית המרחבית של קרינת מקור קרינה איזוטרופי (כדור שלם) ניתן לקרב את הזווית המרחבית Wa בעזרת שני רוחבי אלומה בחתכים אורתוגונליים:
חתכי הקרינה בנוסחה (3) מבוטאים בראדיאנים והזווית המרחבית מבוטאת בסטראדיאנים. כדי לעבור למעלות נחלק את רוחבי האלומה ב- 57.3 ונקבל:
עיקבת הקרינה של האנטנה איננה בדיוק מכפלה של שני רוחבי האלומה אלא היא צרה יותר ודומה לאליפסה חסומה בתוך מלבן (או עיגול חסום בתוך ריבוע). לכן יש להפחית מנוסחה (4) פקטור כלשהו הנתון בקירוב על ידי p/4. בספרים רבים [3] – [1] מקרבים את הכיווניות לפי:
בגישה שונה במקצת, הידועה כקירוב Tai and Pereira [5],[, p.541] מגדירים את כיווניות האנטנה בעזרת שני ערכי כיווניות חלקיים, המתייחסים לשני חתכי הקרינה הראשיים.
Prad הם הספקי הקרינה בשני הקיטובים ואילו Uq , Uf הן צפיפויות הקרינה בהתאמה.
קירוב זה מוביל לניסוח הכיווניות לפי:
כאשר רוחבי האלומה מבוטאים בראדיאנים, או:
אם רוחבי האלומה מבוטאים במעלות.
נתבונן בדוגמה הבאה. באנטנה מסוימת, רוחבי האלומה הם 18°x18° והכיווניות היא 100, כלומר 20 dBi, מכאן לפי (5):
D = 100 = 32,400 / 18 x 18
ולפי (10):
D = 100 = 64,800 / (182 + 182)
רואים שקירוב Tai and Pereira נותן כיווניות גבוהה ב- 0.5 dB לערך ביחס לקירוב Kraus.
- שטח האנטנה
יש להעיר כאן כי אם נציב במקום רוחבי האלומה את נוסחת העקיפה לפי תומאס יאנג:
עבור מפתח מלבני בשטח dx x dy = A המואר באופן אחיד, נקבל:
זהו החסם העליון לכיווניות אנטנה מפני שהוא מבטא הארה אחידה ללא מישקול אמפליטודה ופאזה. כל אנטנה אחרת תהיה בעלת כיווניות נמוכה מהמתואר ב-(12).
חסם אחר המתואר ב- [, p.3783] מציע להכניס את האנטנה לתוך כדור בקוטר D ולאמוד את הכיווניות המכסימלית האפשרית על ידי:
החסם המתואר על ידי הקו האדום באיור 1 [3] מראה למשל כי עבור אנטנה כלשהי החסומה בתוך כדור שקוטרו D = 5l נקבל Do < (5p)2 או פחות מ-24 dBi.
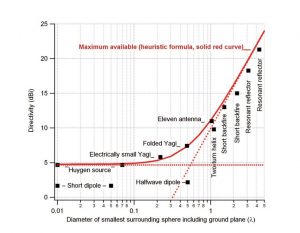
איור 1 חסם של כיווניות אפשרית עבור אנטנה חסומה בתוך כדור שקוטרו D. קרדיט [3]
- שבח האנטנה
השבח של אנטנה מכיל לא רק את תכונת הפיזור הזוויתי של האנטנה אלא גם את הנצילות האנרגטית שלה, כלומר הוא מוגדר על ידי מכפלת הכיווניות בנצילות h:
נצילות אנטנה היא תכונה חמקמקה וקשה למדידה. לעיתים נמנעים מהגדרה ברורה שלה ומכנים את המכפלה 32,000h או 30,000h באות K
נזכיר כי רוחבי אלומה ושבח הן תכונות הניתנות למדידה מדויקת ואילו כיווניות ונצילות הן תכונות מורכבות שקשה למדוד. מכאן שהפקטור K מהווה מדד מקורב לנצילות האנטנה.
- אימותים ניסויים של קירובי הכיווניות
במאמר [7] נבדקו 5 אנטנות שופר מקופלות על שם Hogg. אנטנת Hogghorn המקורית הומצאה על ידי Alfred C. Beck ו-Herald T. Friis במעבדות Bell בניו ג’רסי בשנת 1941. היא נבנתה בשנת 1965 על ידי David C. Hogg באמצעות שופר גדול עם מחזיר פרבולי מובנה בזווית 45 מעלות המכונה “השופר של הולמדל” כמתואר באיור 2 [8]. האנטנה מצטיינת באונות צד נמוכות מאד וביעילות הספק גבוהה. מאוחר יותר האנטנה שימשה לגילוי קרינת הרקע הקוסמית על ידי Penzias ו-Wilson [9].

איור 2 השופר המקורי של HOLMDEL ששימש לגילוי קרינת הרקע הקוסמית. קרדיט [10]

איור 3 יישום שופר Hogg בערוצי מיקרוגל לטווחים ארוכים. קרדיט [11]
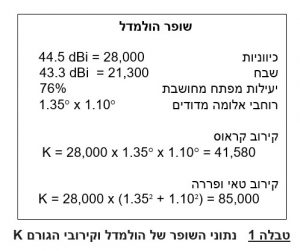
טבלה 1: נתוני השופר של הולמדל וקירובי הגורם K
רואים אפוא כי שופר מיוחד זה אשר הושקעו בו מאמצי פיתוח רבים, נתן שבח גדול ב- 41,580/32,400 = 1 dB ביחס לקירוב קראוס וגדול ב- 85,000/72,815 = 0.7 dB ביחס לקירוב טאי ופררה. היתרון של בדיקת הקירובים לפי שופר זה הוא בכך שנצילות ההספק היא כמעט 1 ויעילות המפתח המחושבת נובעת משגיאות פאזה.
כאמור, החוקרים Dolecek and Schejbal [7] השתמשו בשופרי Hogg פשוטים יותר אך כמעט חסרי הפסדים, כדי לאמוד בדרך ניסויית את הכיווניות מתוך רוחבי האלומה. איור 4 מראה את השבח המדוד של 5 שופרים בתלות בתדר. איור 5 מראה את רוחבי האלומה המדודים ואיור 6 מראה את הכיווניות המחושבת לפי 32,400/qEqH. הפער הממוצע בין נתוני איור 4 לבין נתוני איור 6 הוא 1 dB, ולפיכך המסקנה היא כי הקירוב האופטימלי (באנטנות שופר עם נצילות גבוהה) הוא:

איור 4 השבח המדוד של 5 שופרי Hogg. קרדיט [7]
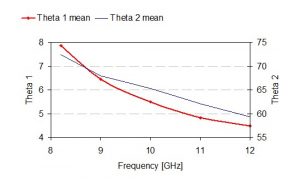
איור 5 רוחבי האלומה המדודים של 5 שופרי Hogg. קרדיט [7]
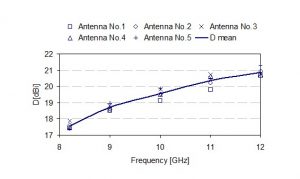
איור 6 הכיווניות המחושבת של 5 שופרי Hogg לפי 32,000/qEqf. קרדיט [7]
בבדיקת מערך 2 אלמנטי מיקרוסטריפ, בתדר 2483 MHz שנערכה במכללת אפקה בתל אביב, התקבלה התוצאה המובאת באיור 7.
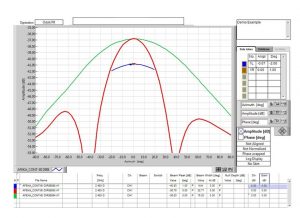
איור 7 שני חתכי קרינה אורתוגונליים המראים רוחבי אלומה של 32.8° x 76.2°ושבח של אנטנת ייחוס מדויקת G = 7 dBi.
במקרה זה נמצא אפוא שבח G = 11.0 dBi = 12.6 ולכן גורם K הוא:
K = 12.6 x 32.8 x 76.2 = 31,400
מידיעה נפרדת של הנצילות לפי h = 0.9 נסיק אפוא כי:
D = 34,800
בבדיקה אחרת, נמדד מערך ריבועי של 2X4 אלמנטי מיקרוסטריפ בתדר 2450 MHz, עם יעילות מחושבת של h=0.8. רוחבי האלומה כמתואר באיור 8 היו 37.5° x 20.1° והשבח היה 15.5 dBi (8.5 dB מעל אנטנת ייחוס של (7 dBi.
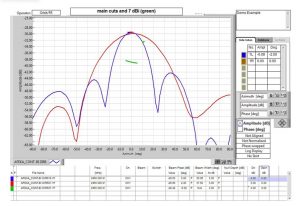
איור 8 שני חתכי קרינה אורתוגונליים המראים רוחבי אלומה של 20.1° x 37.5° ושבח של אנטנת ייחוס מדויקת G = 7 dBi.
במקרה זה גורם K הוא:
K = 35 x 20.1 x 37.5 = 26,380
מידיעת הנצילות h = 0.8 נסיק אפוא כי:
D = 32,970
כלומר באנטנות קטנות יחסית ניתן להשיג מקדמי K קרובים לערך הנומינלי של 32,400.
- מערך כלל כיווני
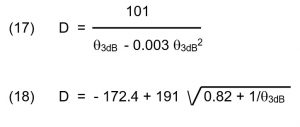
לסיום, נציג שני קירובים עבור מערך קו-לינארי כלל-כיווני שבו קיים מיקוד של אלומת הקרינה רק בהגבהה [[1, p.55. קירוב McDonald [12] בנוסחה (17) ןקירוב Pozar [13] בנוסחה (18) כדלקמן:
נתאר למשל אנטנה כלל כיוונית עם שבח 9 dBi של חברת Alfa [14] שבה רוחב האלומה בהגבהה (איור 9) הוא 16°.

איור 9 חלק מקטלוג Alfa AOA-2409 TFA. רוחב האלומה בהגבהה בנקודות 3 dB הוא 16°. קרדיט [12]
אילו היינו מחלקים את זווית ההגבה השלמה של 180° ברוחב האלומה של האנטנה °16 ומכפילים ביעילות של 0.8, ניתן היה לצפות לשבח של 0.8 x 180/16 = 9 = 9.5 dBi , אך לפי קירוב (17) מקבלים D = 8.3 dBi ולפי קירוב (18) מקבלים D = 8.5 dBi. שני הקירובים מגיעים אפוא לאותה מטרה וכך גם ניתן לראות באיור 10 [ [1,p.57.
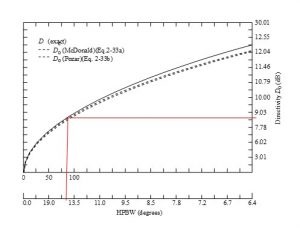
איור 10 אנטנה כלל כיווניות, הכיווניות בתלות ברוחב האלומה. הנקודה המסומנת באדום מתאימה לאנטנת Alfa המתוארת לעיל. קרדיט [1]
מראי מקום
[1] C.A. Balanis, Antenna Theory – Analysis and Design, Wiley 2015.
[2] T.A. Milliganm, Modern Antenna Design, Wiley 2005.
[3] P.S. Kildal, Foundations of Antenna Engineering, Kildal Anten 2017.
[4] V. Schejbal, “Directivity of Planar Antennas”, IEEE AP Magazine, Vol. 41, No.2, pp.60-62, 1999.
[5] W.L. Stutzman, Estimating Directivity and Gain of Antennas”, IEEE AP Magazine, Vol. 40, pp. 7-11, 1998.
[6] C.T. Tai and C.S. Pereira, “An Approximation Formula for Calculating the Directivity of an Antenna”, IEEE AP-24, No.2, pp. 235-236, 1976.
[7] R. Dolecek and V. Schejbal, “Estimation of Antenna Gain”, IEEE AP Magazine, Vol. 51, pp. 124-125, 2009.
[8] Crawford, A.B. , D.C. Hogg and L.E. Hunt. “Project Echo: A Horn-Reflector Antenna for Space Communication,” The Bell System Technical Journal, pp. 1095-1099, July 1961.
[9] Penzias,A.A., and R. W. Wilson. “A Measurement of the Flux Density of CASA At 4080 Mc/s,” Astrophysical Journal Letters, pp. 1149-1154, May 1965.
[10] Atlas Obscura
[11] Western electric microwave antennas
[12] N.A. McDonald, “Approximate Relationship Between Directivity and Beamwidth for Broadside Colinear Arrays”, IEEE AP-26, No. 3, pp. 340-341, 1978.
[13] D.M. Pozar, “Directivity of Omnidirectional Antennas”, IEEE Magazine, Vol. 35, No. 5, pp.50-51, 1993.
[14] www.alfa.com.tw