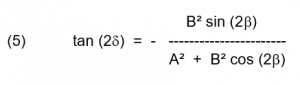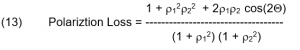. קיטוב של גל אלקטרומגנטי
קיטוב (polarization) הוא תכונה כללית של כל גל אלקטרומגנטי המתפשט במרחב ומשמעותה היא הכיוון של וקטור השדה החשמלי בתלות בזמן. היות וגל אלקטרומגנטי במרחב משודר ונקלט על ידי אנטנות כלשהן הרי ניתן לייחס את תכונת הקיטוב של הגלים במרחב לאנטנות עצמן.
נתאר את השדה החשמלי המשודר או נקלט באנטנה כלשהי כסכום וקטורי של שני שדות ניצבים זה לזה EΦ, Eθ (הסימונים לקוחים מן הספר הקלאסי של R.S. Elliot [1]):
(1) E = [1θ Eθ + 1Φ EΦ] exp (jωt)
1θ, 1Φ הם וקטורי יחידה בצירים θ,Φ ואילו Eθ, EΦ הם השדות החשמליים בכיוונים θ,Φ. נצמצם את הדיון לשדות חשמליים ממשיים התלויים רק בקואורדינטותθ,Φ,r ונרשום:
(2) E = 1θ A cos(ωt + a) + 1Φ B cos (ωt + b)
היכן ש: A,B הן אמפליטודות השדה החשמלי ואילו a,b הן הפאזות של השדה החשמלי. מבלי לפגוע בכלליות נוכל לקבוע ש: a=0 ולכן:
(3) E = 1θ A cos(ωt) + 1Φ B cos (ωt + b)
הקיטוב הוא אפוא קו דמיוני במרחב המוכתב על ידי קצה הוקטור החשמלי. הקיטוב מאונך לכיוון השדה המגנטי ולכיוון ההתפשטות. למעשה, הקיטוב הכללי ביותר הוא אליפטי והיחס בין הצירים הראשי והמשני נקרא יחס צירי Axial Ratio. אם ציר אחד הוא קטן מאד ביחס לציר השני, הקיטוב הוא לינארי. אם שני הצירים שווים הקיטוב הוא מעגלי. איור 1 מציג את התנועה הספירלית של קצה הוקטור החשמלי של גל מקוטב מעגלית ואת אליפסת הקיטוב (ההיטל של תנועת הגל על מישור) [2].
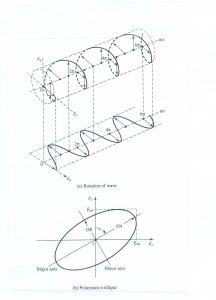
איור 1: תנועת הוקטור החשמלי של גל מקוטב ואליפסת הקיטוב
- קיטוב אליפטי
המקרה הכללי ביותר הוא כאשר A ¹ B וb- אקראי. דרך אגב, אם b = 0 שני הוקטורים הניצבים יוצרים וקטור שקול אלכסוני ואז הקיטוב הוא לינארי אבל מסובב. במקרה של הקיטוב האליפטי אפשר להראות כי קצה השדה החשמלי מסתובב בזמן לאורך היקף אליפסה וערכו המוחלט של השדה החשמלי יהיה:
(4) |E| = [ A² cos² (ωt) – B² cos² (ωt – β)] 1/2
השדה יקבל ערכים מכסימליים ומינימליים בנקודות שבהן ωt = δ המתקבלות ע”י:
רמת האליפטיות של הקיטוב מוגדרת לפי היחס בין השדה המכסימלי בריבוע לבין השדה המינימלי בריבוע לאורך האליפסה. יחס זה נקרא יחס צירי ((Axial Ratio ובמקרים מסוימים ערך ייחוס כגון AR = 3 dB מהווה תנאי לעמידת האנטנה ברמת ביצועים נדרשת. לקיטוב שבוAR מסדר גודל 3 dB ואף 6 dB עדיין קוראים “קיטוב מעגלי”. לקיטוב שבו AR הוא מסדר גודל של 10 dB מתייחסים כבר כאל קיטוב לינארי עם מרכיב כלשהו של קיטוב ניצב (Cross Polarization). הקיטוב הניצב הוא אפוא היחס בין קיטוב מעגלי ראשי לקיטוב מעגלי משני. קיים קשר בין שני הפרמטרים כדלקמן [3]:
(6) Cross pol = (√AR – 1)² / (√AR +1)²
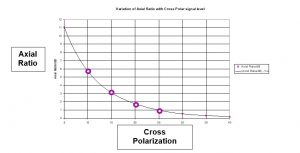
איור 2: הקשר בין קיטוב ניצב לבין יחס צירי
דוגמאות: AR = 6 dB ↔ cross = 10 dB
AR = 3 dB ↔ cross = 15 dB
AR = 2 dB ↔ cross = 20 dB
AR = 1 dB ↔ cross = 25 dB
- קיטוב לינארי
קיטוב לינארי בכיוון θ מתקבל אם B=0 וקיטוב לינארי בכיוון Φ מתקבל אם A=0. באופן מעשי נוח להגדיר ולהפריד בין קיטוב אנכי לבין קיטוב אופקי, אך אלו הן הגדרות הקשורות להצבה המרחבית של האנטנה ולא לתכונת הקרינה הבסיסית שלה. במצב שבו האנטנה היא אלמנט זרם אנכי (כגון: דיפול או מונופול) או אלמנט שדה אנכי (כגון: קצה גלבו או אלמנט מיקרוסטריפ עם הזנה בקצה אחד) נאמר שהאנטנה משדרת או קולטת בכיוון אנכי, אבל ברור שאם נסובב את האנטנה סביב ציר הקרינה (r) ב-90 מעלות אזי הקיטוב שלה יהיה אופקי. אנו מבינים אפוא שלאנטנה יש קיטוב לינארי כללי אך כאשר מציבים את האנטנה במרחב מתקבלת ההבחנה בין קיטוב אנכי לבין קיטוב אופקי.
- קיטוב מעגלי
קיטוב מעגלי מיוצר על ידי שני אלמנטי זרם שווים בגודלם עם הפרש פאזה קבוע של 90 מעלות. כמו כן נדרש ששני אלמנטי הזרם יהיו ממוקמים בדיוק באותו מקום. הדרישה הזאת אינה פשוטה למימוש ולכן קיטוב מעגלי מעשי אינו מושלם, כלומר האליפסה אינה הופכת למעגל.
אם A = B וגם β = -90° אזי:
(7) E = A[1θ cos(ωt) + 1Φ sin(ωt)]
ואז אפשר לומר שקצה השדה החשמלי מסתובב בזמן לאורך עיגול במהירות w וקיטוב הגל (או האנטנה) הוא מעגלי ובו בזמן השדה החשמלי מתקדם בכיווןr כמתואר באיור 1. היות וכיוון הסיבוב, כאשר האנטנה משדרת, הוא בכוון השעון נכנה את הקיטוב המעגלי הזה בשם קיטוב ימני (Right Hand Circular Polarization) ואילו במקרה של A = B וגם b = 90° אזי:
(8) E = A[1θ cos(ωt) – 1Φ sin(ωt)]
קיטוב זה נקרא בשם קיטוב שמאלי Left Hand Circular Polarization. התנאי הכללי להווצרות קיטוב מעגלי באנטנה הוא כאמור קיומם של שני רכיבי זרם (או שדה) ניצבים זה לזה, בעלי אמפליטודה שווה והפרש פאזה של 90° או -90°.
דוגמאות לטכניקות מימוש אנטנות בקיטוב מעגלי מובאות באיור 3.
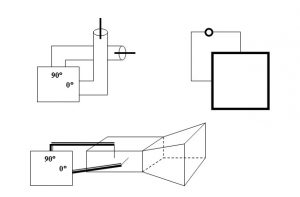
איור 3 דוגמאות למימוש אנטנות בקיטוב מעגלי: זוג מונופולים ניצבים, אלמנט מיקרוסטריפ ריבועי עם שתי הזנות ניצבות ושופר עם שתי נקודות הזנה ניצבות. בכל המקרים שתי ההזנות נמצאות בהסחת פאזה של 90 מעלות. היפוך ההזנות ממיר את הקיטוב המעגלי מימני לשמאלי
- הפסדי קיטוב
הפסדי קיטוב Polarization Loss מיוחסים להצבה היחסית של המקלט ושל המשדר בערוץ התקשורת, או להסחה היחסית של הקיטוב של הגל האלקטרומגנטי המתפשט במרחב. ראשית נתייחס למצב הפשוט יותר של אנטנות שידור וקליטה בקיטוב לינארי המסובבות אחת ביחס לשניה. הפסד הקיטוב במקרה זה (ביחידות הספק) יהיה קוסינוס בריבוע של זווית הסיבוב בין האנטנות אשר נסמן אותה ב-ψ.
(9) Polarization Efficiency (2 linear antennas) = cos²(ψ)
בקיטוב מעגלי יעילות הקיטוב היא:
(10) Polarization Efficiency = 1 / [1+(√AR–1)²/(√AR+1)²]
אם בערוץ שידור כלשהו אנטנה אחת היא לינארית והאנטנה השניה היא בקיטוב מעגלי, אזי אפשר לומר שקצה השדה החשמלי של אנטנה אחת מסתובב במהירות רבה ומוטל על קצה של שדה חשמלי שאינו משתנה בזמן. הממוצע של שדה חשמלי המשתנה מהר הוא כידוע 0.5 ולכן ניתן לקבוע כי הפסד הקיטוב יהיה 3 dB.
(11) Polarization Loss (linear vs. circular antennas) = 3 dB
טבלה 1 מסכמת את הפסד הקיטוב בין משדרים ומקלטים בקיטובים לינאריים ומעגליים. נשים לב שערכי ההפסד נתונים ביחידות dB כך שהעדר הפסדים הוא 0 dB והפסד מוחלט הוא ∾ dB. טבלה זו מניחה שהקיטובים הם מושלמים אבל בחיי המעשה נדרש להעריך גם את הפסדי הקיטוב בין משדרים ומקלטים לא אידאליים ובכך נעסוק להלן.
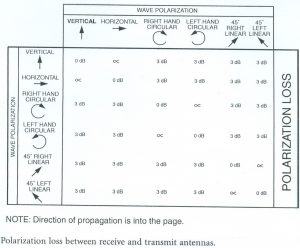
טבלה 1: הפסדי קיטוב בין אנטנות בקיטוב לינארי ומעגלי
נתאר אפוא את המצב הכללי של אנטנת שידור עם קיטוב מעגלי לא מושלם המוגדרת על ידי היחס הצירי AR1 ואנטנת קליטה עם קיטוב מעגלי לא מושלם המוגדרת על ידי היחס הצירי AR2. הזווית היחסית של צירי האליפסה בשתי האנטנות היא θ [4].
נגדיר משתני ביניים r1,r2 כדלקמן:
(12) ρ1 = (AR1 +1) / (AR1 – 1)
ρ2 = (AR2 +1) / (AR2 – 1)
ומכאן נחלץ [5] את הפסד הקיטוב בין שתי אנטנות בקיטובים מעגליים לא מושלמים:
רואים שהפסד הקיטוב תלוי בזווית היחסית בין שתי אליפסות הקיטוב. ההפסד המכסימלי הוא כאשר cos(2θ) = 1 וההפסד המינימלי הוא כאשר cos(2θ) = -1.
דוגמאות לחישוב הפסד מכסימלי והפסד מינימלי (שני הקיטובים ימניים או שמאליים) מובאות בטבלה 2 כדלקמן:
AR1 AR2 Max Loss Min Loss
——————————————————————–
3 dB 0 dB 0.1 dB 0.05 dB
3 dB 3 dB 0.5 dB 0.1 dB
6 dB 0 dB 0.6 dB 0.4 dB
6 dB 3 dB 1.2 dB 0.2 dB
6 dB 6 dB 2.0 dB 0.1 dB
טבלה 2 הפסדי קיטוב בין אנטנות בקיטובים מעגליים לא מושלמים (זהים)
רואים שיחס צירי 3 dB ואף 6 dB אינו גורם להפסד קרינה משמעותי מדי אם שני הקיטובים ימניים או שמאליים. בספרות אפשר למצוא מחשבונים גרפיים לאומדן מהיר של הפסדים אלו, למשל המובאים באיורים 3-4.
דוגמאות לחישוב הפסד מכסימלי והפסד מינימלי (שני הקיטובים הפוכים – ימני כנגד שמאלי) מובאות בטבלה 3 כדלקמן:
AR1 AR2 Max Loss Min Loss
——————————————————————–
3 dB 0 dB 15 dB 15 dB
3 dB 3 dB 27 dB 10 dB
6 dB 0 dB 10 dB 10 dB
6 dB 3 dB 16 dB 7 dB
6 dB 6 dB 20 dB 5 dB
טבלה 3 הפסדי קיטוב בין אנטנות בקיטובים מעגליים לא מושלמים (הפוכים)
רואים שאם הקיטובים הפוכים הפסדי הקיטוב גבוהים מאד. בספרות אפשר למצוא מחשבונים גרפיים לאומדן מהיר של הפסדים אלו, למשל כמו באיורים 4-5.
במקרה אחר, נוכל להציג את ההפסד של קיטוב אליפטי כנגד קיטוב מעגלי מושלם, כמתואר בטבלה 4.
AR1 AR2 Loss for all Q
————————————————–
0 dB 0 dB 0 dB
0 dB 2 dB 0 dB
0 dB 3 dB 0.1 dB
0 dB 4 dB 0.2 dB
0 dB 5 dB 0.3 dB
0 dB 6 dB 0.5 dB
0 dB 8 dB 0.8 dB
0 dB 10 dB 1.1 dB
0 dB 14 dB 1.6 dB
0 dB 20 dB 2.3 dB
טבלה 4 הפסדי קיטוב בין אנטנות בקיטוב מעגלי נקי וקיטוב אליפטי
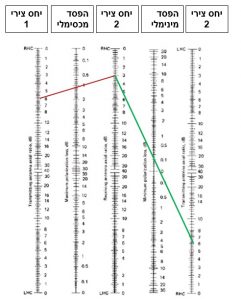
איור 4: מחשבון גרפי לאומדן הפסדי קיטוב בין שתי אנטנות עם קיטובים מעגליים לא מושלמים. הקו האדום מראה את המקרה של RHCP with AR = 3 dB כנגד RHCP with AR = 6 dB לקבלת הפסד מכסימלי של 1.2 dB הקו הירוק מראה את המקרה של RHCP with AR = 3 dB כנגד RHCP with AR = 6 dB לקבלת הפסד מינימלי של 0.2 dB. קרדיט [5]

איור 5: מחשבון גרפי לאומדן הפסדי קיטוב בין שתי אנטנות עם קיטובים מעגליים לא מושלמים. הקו הכחול מראה את המקרה של RHCP with AR=6 dB כנגד LHCP with AR = 3 dBלקבלת הפסד מכסימלי של 20 dB הקו הסגול מראה את המקרה של RHCP with AR = 3 dB כנגד LHCP with AR = 6 dB לקבלת הפסד מינימלי של 6.5 dB. קרדיט [5]
[1] R.S. Elliott, Antenna Theory and Design, John Wiley, 2003.
[2] C.A. Balanis, Antenna Theory – Analysis and Design, Wiley 2015.
[3] J.D. Kraus and R.J. Marhefka, Antennas, McGraw Hill, 2001.
[4] S. Gao, Q. Luo and F.Zh, Circularly Polarized Antennas, J. Wiley and sons, 2014.
[5] R. Galuscak and P. Hazdra, Circular Polarization and Polarization Losses CTU Prague, FEE, Dept. of Electromagnetic Field, Technicka 2, 166 27, Prague, Czech Republic, E-mail:, om6aa@yahoo.com, hazdrap@fel.cvut.c