הקדמה
עיקרון השקילות האלקטרומגנטית Electro-Magnetic Equivalence הוא אחד הכלים התיאורטיים היסודיים בהבנת ובפתרון משוואות מכסוול Maxwell. נציג כאן את העיקרון הבסיסי הקשור לתורת הפיזור של הויגנס Huygens ופרנל Fresnel, שעל פיו ניתן להמיר גוף עם זרמים נפחיים בגוף שקול עם זרמים משטחיים בלבד. נסקור גם שתי גירסאות מודרניות יותר – של Augustin Edward Hough Love (המייצרת שקילות אל גוף אידאלי שבו השדה החשמלי והמגנטי מתאפסים) ושל Sergei Alexander Schelkunoff (המניחה גוף אשר השפה שלו מוליכה זרם חשמלי באופן אידאלי Perfect Electric Conductor או לחילופין, השפה שלו מוליכה זרם מגנטי באופן אידאלי (Perfect Magnetic Conductor.
נזכיר כאן כי כאשר מתייחסים באופן כללי ל”עיקרון השקילות” מתכוונים בדרך כלל לשקילות פיזיקלית כפולה על פי תיאוריות היחסות של אלברט איינשטיין. מצד אחד מבחינים בשקילות על פי היחסות הפרטית בין מסה לאנרגיה E=mc2 (כגון בעירת השמש ההופכת גז מיונן לקרינה אלקטרומגנטית או התנגשות בין חלקיק ואנטי חלקיק המייצרת אנרגיה). מצד שני מבחינים בשקילות על פי היחסות הכללית בין מערכת הנמצאת בתאוצה עקב כוח קינטי לבין מערכת הנמצאת בשדה כבידה (כגון אדם פלאי הנמצא במעלית סגורה מואצת ואינו יודע אם המעלית מואצת עקב פעולת המנוע או בגלל כוח גרביטציה). מסגרת דיוננו כאן היא צנועה יותר ומתייחסת רק לשדות ולזרמים חשמליים ומגנטיים.
- משוואות מכסוול
משוואות מכסוול הן מערכת של 4 משוואות דיפרנציאליות הקושרות בין מקורות הקרינה לבין שדות הקרינה באופן שלם. המשתנים הבסיסיים הם:
השדה החשמלי E
ההעתקה החשמלית D
השדה המגנטי H
ההעתקה המגנטית B
צפיפות המטענים ρ
צפיפות הזרם החשמלי J

ג’יימס קלרק מכסוול 1850-1929
בתווך לינארי מבחינה חשמלית קיים :
(1) D = εo εr E
היכן ש-ε = εoεr הוא המקדם הדיאלקטרי.
בתווך לינארי מבחינה מגנטית קיים:
(2) B = μo μr H
היכן ש-μ = μoμr הוא המקדם הפרמיאבילי.
כמו כן משוואת הרציפות קובעת:
4 משוואות מכסוול בצורתן הדיפרנציאלית נכתבות כדלקמן:
בהנחה של תלות הרמונית בזמן ובתווך לינארי מתקיים :
(8) Curl E = -jωμH
(9) Curl H = J + jωεE
(10) Div E = ρ/ε
(11) Div H = 0
4 משוואות מכסוול בתווך לינארי הן ריכוז מתמטי מתומצת ודייקני של משוואת פאראדיי ((curl E, משוואת אמפר ((curl H ושתי משוואות גאוס ((DIV.

אנרי מארי אמפר 1775-1836

מיכאל פאראדיי 1791-1867
המשמעות המעשית של הדיברגנס היא שאם Div H ¹ 0 בנקודה כלשהי, אזי יש שטף פליטה או קליטה מהנקודה הנדונה. אם Div H = 0 אזי הנקודה היא נקודת שבת ואין בה פליטה או קליטה, לכן הדיברגנס מראה כמה קרינה יש בנקודה. המשמעות המעשית של הרוטור (curl) היא עד כמה השדה בנקודה מסוימת נטוי סביב עצמו. דוגמה לחלוקה של מרחב סופי סביב נקודה ע”י משולשים מובאת באיור 1.

איור 1 בדיקת הסיבוב של הנקודה במרחב על ידי רוטור. קרדיט [2]
קרל פרידריך גאוס 1777-1855
כבר עם ניסוח המשוואות השונות הקושרות בין שדות חשמליים ושדות מגנטיים, הועלתה במלוא חריפותה השאלה האם הדואליות הגבוהה בין תפקוד שני המשתנים היא מקרית או מצביעה על קשר עמוק ביניהם. לא לחינם השדות האלו נקראים שדות “אלקטרו-מגנטיים”, כלומר קיימת דואליות בין שדה מסוג אחד לבין שדה מסוג שני. האם מדובר בשתי תופעות או בתופעה אחת עם שני פנים ?
יש לציין כי קיומה של דואליות בין שני משתנים, כלומר הרעיון התיאורטי ששניהם מתנהגים באופן סימטרי זה ביחס לזה בתנאים מסוימים, עדיין אינה מבטיחה את קיומה של שקילות מתמטית, כלומר שאפשר לפתור משוואה אחרת ולהגיע בדיוק לאותה תוצאה. הטיפול המתמטי בבעית הדואליות האלקטרומגנטית הותנע כבר במאה ה-17 על ידי הויגנס ופרמה (“שקילות הויגנס – פרמה“) אשר טענו כי חזית הגל כוללת אינסוף נקודות עירור דמיוניות, שכל אחת מהן היא מקור גלים עצמאי. העקיפה וההתאבכות על פני חזית הגל יכולים להסביר את כל תופעות הגלים המוכרות לנו.

כריסטיאן הויגנס 1629-1695

אוגוסטין ז’אן פרנל 1788-1827
- עקרון השקילות
עיקרון השקילות נולד אפוא עקב הדמיון הרב בין השדה החשמלי והשדה המגנטי במשוואות ההתפשטות של שדות קרינה. כדי לבסס את השקילות הומצא מושג חדש של זרם מגנטי M שאינו קיים במציאות ומטען מגנטי rm שאינו קיים במציאות אך הם משלימים את הסימטריה. כמו כן נזכור כי אימפדנס הגלים הוא:
(12) η = √μ/ε
וכי מספר הגל הוא (13) kc = 2π/λ
מספר הגל מקיים את הקשר kz2 = ω²με + 2(14) kx2 + ky
כאשר:
מספרי הגל בכל כיוון kx ky kz
תדירות זוויתית ω
תדירות רגילה f
אורך גל באוויר λ
צפיפות המטענים ρ
צפיפות הזרם החשמלי J
כעת נוכל לרשום את משוואות מכסוול מחדש עם סימטריה מלאה.
(15) Curl E = -jωμH – M
(16) Curl H = jωeE + J
(17) Div εE = ρ
(18) Div μH = ρm
כזכור, בפתרון ההרמוני, נגזרת בזמן פירושה הכפלה ב–jω . עיקרון השקילות על פי הויגנס–פרנל יטען מעתה כי כל נקודה על פני חזית הגל היא מקור זרם עצמאי המסוגל להציג את השדה ותוצאותיו בצורה אחת ויחידה, ומתאימה לכל שיטת פתרון אחרת. עקרון יחידות הפתרון הוא אבן דרך הכרחית בדרך מדואליות לשקילות.
טענת השקילות ניתנת להצגה בשתי דרכים. באיור 2 אנו רואים את מקרה השקילות פנימה–החוצה. הגוף (a) כולל זרם חשמלי נפחי J וזרם מגנטי נפחי M. הבעיה שקולה לגוף (b) הכולל זרם חשמלי משטחי Js וזרם מגנטי משטחי Ms והשדות בתוך הגוף מתאפסים.
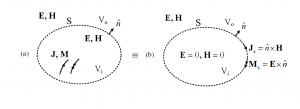
איור 2 עקרון השקילות היסודי פנימה – החוצה
באיור 3 אנו רואים את מקרה השקילות החוצה – פנימה. בגוף (a) פוגעים זרמים נפחיים חשמליים J ומגנטיים M. הזרמים מותמרים באופן יחיד לגוף (b) שבו קיים זרם משטחי חשמלי Js וזרם משטחי מגנטי Ms ואין שדות נפזרים במרחב.
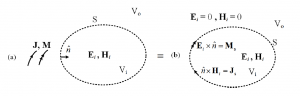
איור 3 עקרון השקילות היסוד החוצה – פנימה
השליפה של הזרמים המשטחיים ניתנת לסיכום מתוך שני תנאי שפה נפרדים:
(19) Js = n x (H1 – H)
(20) Ms = – n x (E1 – E)
J,M זרמים אמיתיים (אם כי M איננו ניתן למדידה), Js,Ms הם מדומים (מומצאים), E,H שדות מומצאים בתוך הגוף, E1,H1 הם שדות אמיתיים מחוץ לגוף.
נמצאנו למדים על טבלת שקילות מוכללת גם בין שדות וזרמים וגם בין קואורדינטות, מספרי גל, אימפדנסים ופוטנציאלים וקטוריים.
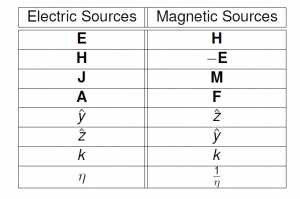
טבלה 1 טבלת דואליות אלקטרומגנטית
ועתה נשלים לגבי משואות מכסוול ולגבי הפוטנציאלים הוקטוריים.
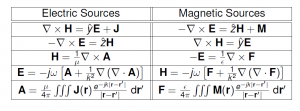
טבלה 2 טבלת שקילות אלקטרומגנטית
כל בעיה אלקטרומגנטית ניתנת בודאות להצגה בין על ידי הטור הימני ובין על ידי הטור השמאלי. בחירת הפורמט היא לחלוטין ענין של נוחות והקלה בכמות החישובים.
- הרחבות על שם Love – Schelkunoff
עיקרון השקילות נוסח מחדש על ידי Love בשנת 1901 במונחים של תנאי שפה נוחים לטיפול (איור 4). הוא בחר להחליף זרמים נפחיים בתוך גוף כלשהו J,M, בזרמים משטחיים Js,Ms על פני גוף שקול, כך שהשדות החשמליים בתוך הגוף E,H יתאפסו. בחירה זו מפשטת מאד את החישובים ומקלה על ביצוע השקילות בפועל.

אוגוסטין אדוארד יוז לאב 1863-1940
גישה שונה במקצת לניסוח תנאי השפה הוצעה על ידי שלקונוף בשנת 1936. הוא החליף את הגוף השקול בגוף דמיוני עשוי מתכת מושלמת שקרא לה PEC Perfect Electric Conductor ובה השדות מתאפסים. על פני הגוף קיים זרם משטחי מגנטי בלבד Ms. הוא ניסח גם שקילות אחרת אל גוף דמיוני עם מעטפת מגנטית מושלמת בשם PMC Perfect Magnetic Conductor ועליה קיים זרם משטחי חשמלי בלבד Js. שני המודלים של שלקונוף מאפשרים הקלה בחישובים מסוגים רבים.
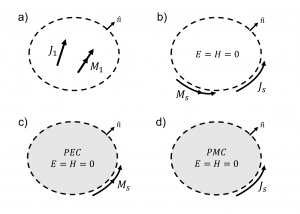
איור 4 עקרון השקילות בגירסאות מודרניות
(a) הגוף המקורי
(b) הגוף השקול על פי Love
(c) גוף שקול על פי Schelkunoff מסוג PEC
(Perfect Electric Conductor)
(d) גוף שקול על פי Schelkunoff מסוג PMC
(Perfect Magnetic Conductor)
- סיכום
עיקרון השקילות הוא הרחבה מודרנית של תורת הפיזור הקלאסית של הויגנס-פרנל. הויגנס ניסח זאת כך – כל אלמנט של חזית גל אפשר להציג כמרכז פאזה של גל חדש שיתקדם במרחב בכל זמן עתידי. פרנל הרחיב וטען שהגלים המשניים יכולים להתאבך ביניהם אם קיימים מכשולים בין המקור ונקודת התצפית. לאב הציע מנגנון שקילות נוח לעבודה, כך שבתוך הגוף השקול אין שדות כלל ושלקונוף הציע שני מודלים של גוף מוליך חשמלי מושלם ושל גוף מוליך מגנטי מושלם. בכל הגירסאות האלו ובפיתוחים נוספים שהוצעו מאז, קיים שילוב בין רעיון הסימטריה בין השדה החשמלי והמגנטי (או בין הזרם החשמלי הממשי והזרם המגנטי המדומיין) לבין עקרון אחידות הפתרון שמשמעותו עקרון השקילות – היכולת להחליף שיטת פתרון אחת בשיטת פתרון אחרת ולקבל בדיוק אותה תוצאה. לעקרון השקילות יש חשיבות רבה בפתרונות נומריים של בעיות קרינה – תכן אנטנות, פיזור ממשטחים, משטחים מלאכותיים ופלזמונים והיא גם בסיס עיקרי בהקלת החישובים בשיטת המומנטים.
- מראי מקום
[1] Wikipedia, Surface Equivalence Principle.
[2] W.C. Chew, Lectures on Electromagnetic Field Theory, Purdue University, 2020.
[3] S. Aksoy, Advanced Electromagnetic Theory, Lecture Notes, 2012.
[4] B.D. Popovic, “Electromagnetic Field Theorems”, Proc. IEEE 128, 47-63, 2018.
[5] R. Lian, “On Huygens Principle, Extinction Theorem and Equivalence”, HP, ET and EP, 1-21, 2018.
[6] D.S. Weile, “Electromagnetic Theorems”, Lecture Notes ELEG 648, University of Delaware.
[7] P.S. Kildal, Foundations of Antenna Engineering, Kildal Anten AB, 2015.
[8] R.F. Harrington, Time-harmonic Electromagnetic Fields, McGraw-Hill, 1961.
[9] R.F. Harrington, Field Computation by Moment Methods, Macmillan, New York, 1968.
[10] L.B. Felsen and N. Marcuvitz, “Radiation and scattering of waves”, Prentice-Hall, New Jersey, 1973.
[11] C. Huygens Trait`e de Lumiere, Leyden, 1690. English translation by S.P. Thomson (London, Macmillan & Co.), 1912.
[12] G. Kirchhoff, Berl. Ber, p. 641, 1882; Ann. D. Physik , 2, Bd. 18, p. 663, 1883; Ges. Abh. Nachtr., p. 22. 1883.
[13] J. C. Maxwell, “A dynamical theory of the electromagnetic field,” Philosophical Transactions of the Royal Society of London, no. 155, pp. 459–512, 1865.
[14] A.E.H. Love, “The Integration of the Equations of Propagation of Electric Waves”, Philisophical Transactions of the Royal Society A 197 (287-299) ,1901.
[15] S.A. Schelkunoff, “Some Equivalence Theorems of Electro magnetics and Their Application to Radiation Problems”, Bell Labs Technical Journal, 15 (1) 92-112, 1936.
[16] S.A. Schelkunoff, “On Diffraction of Electromagnetic Waves”, Physical Review, 56 (4), 308-316, 1939.
[17] E. Martini, G. Carli, S. Maci, “An Equivalence Theorem Based on the Use of Electric Currents Radiating in Free Space” IEEE Antennas and Wireless Propagation Letters, Vol. 7, pp. 421-424, November 2008.

















