מאת: Vyacheslav M Ryaboy, Newport Corp .שאלות רבות בנושא חלוקת עומסים ויציבות סטטית של מערכות תמיכה פניאומטיות אינן מובנות תמיד כהלכה כאשר מדובר על פלטפורמות משככות רעידות, כתוצאה מכך עלולים להיווצר קשיים בהקמת מערכות אופטרוניות מודרניות.
שולחנות אופטיים על רגליים פניאומטיות הינם פריט הכרחי בבקרת רעשים מדויקת. מלבד שיכוך רעידות מעולה, הם מספקים קיבולת עומס גבוהה המאפשרת לחוקרים לבודד מערכות אופטואלקטריות גדולות, כולל אלמנטים כבדים כגון קריוסטט, לייזרים עוצמתייים, מיקרוסקופי כוח אטומי ( AFM), מיקרוסקופ מינהור סורק ומרכבים אופטיים.
בייצור או הגדרת מפרט של מערכת לשיכוך רעידות, הצעד הראשון הוא לוודא שהעומסים על כל אחד מהרגליים המשככות אינם עולים על הקיבולת המותרת. עבור כל המשככים הוגדרו עומסים מירביים. עבור חלק מהדגמים הוגדרו עומסים מזעריים מומלצים. רוב דגמי המשככים – הפניאומטיים במיוחד – אינם מיועדים לעמידה בעומסים שליליים (מאמץ מתיחה) כלשהם, ולכן יש להעריך את העומסים על כל רגל מראש.
למרבה המזל, מערכות שיכוך פניאומטי חדשניות מוגדרות סטטיסטית תמיד, מה שהופך את חישוב העומס למשימה פשוטה. הן מצוידות בשסתומי יישור להקמת השולחן במיצוב אופקי מדויק, ושומרות על מיצוב זה כנגד שינויים בעומס או הפרעות חיצוניות. בכל עת ישנם שלושה שסתומי יישור, ללא קשר למספר המשככים (Isolators).
פירושו של דבר הוא שחלק מהמשככים (Isolators) משועבדים יחדיו – כלומר, נפחי האויר שלהם מחוברים זה לזה. כאשר מתרחשת הפרעה, הם יכולים להחליף בינהם את האויר בחופשיות, ועל כן אינם מהווים התנגדות לסיבוב המרכז המשותף שלהם. דרכים סטנדרטיות לחיבור המשככים בתצורות אופייניות מתוארות באיור 2.
לחץ האויר זהה בכל משכך של הקבוצה המשועבדת יחד, כך שכל מבודד נושא באותו העומס ונמצא באותו מצב קשיחות. קבוצה של מבודדים משועבדים יחדיו מקבילה איפוא סטטיסטית למבודד אחד הממוצב במרכזו הגיאומטרי, כאשר הקשיחות שווה לסכום הקשיחות הפרטנית. כתוצאה מזאת, בפועל ישנן תמיד שלוש נקודות תמיכה, והמערכת מוגדרת סטטית. על מנת לחשב את העומסים שעל כל מבודד, מספיק לפתור שלוש משוואות שיווי משקל עבור סך העומסים שעל שלוש קבוצות מבודדים, ולחלק את התוצאה במספר המבודדים בקבוצה. מרכז הכבידה (CG)
של קבוצת השולחן כולה והמטען צריך להשאר תמיד במסגרת “משולש היציבות” שבמישור האופקי. במערכת מתוכננת היטב, עומסים הנתמכים על ידי כל המבודדים הינם במסגרת הטווח המותר, ומוטב שיהיו קרובים זה לזה.
ישנם שני סוגים של אי יציבות במערכות בידוד פניאומטיות. הראשון הינו מערכת שהופכת לבלתי יציבה סטאטית, מכיוון שמרכז הכבידה שלה גבוה מדי. והשני המערכת עשויה להפוך לבלתי יציבה דינאמית, מכיוון שההגבר של שסתומי היישור כוון לערך גבוה מדי.
מאמר זה דן בעיקר ביציבות הסטטית. מערכות בידוד בביצועים גבוהים מאופיינות בקשיחות נמוכה מאוד של המבודדים. במערכות בידוד פניאומטיות מהעדכניות ביותר, עשוי להיות רטט טבעי בתדרים נמוכים עד 1
Hz. בכך מתאפשרת אי יציבות סטטית אם מרכז הכבידה של המטען גבוה יחסית. ולכן יש לנתח חוסר יציבות סטטית טרם בניית מערכת הבידוד.
כלל אצבע לכך שמערכת מכנית נמצאית בשיווי משקל סטטי יציבה הוא כאשר כל סטיה קלה ממצב זה גורמת לאנרגיה פוטנציאלית לעלות (איור 3). על פי רוב, האנרגיה הפוטנציאלית היא פונקציה ריבועית (תבנית ריבועית) של סטיות קלות של הקואורדינטות המוכללות מערכי שיווי המשקל. שיווי המשקל יציב כאשר התבנית היא חיובית.
קשיחות לינארית-סטטית וקוואזי-סטטית של תא מבודד רטט פניאומטי מוגדרת על ידי שטח הבוכנה בפועל, הנפח הכולל, הלחץ האטמוספרי והלחץ היחסי. בהערכת קשיחות המבודד תחת הפרעות קלות למטרת חישוב בידוד הרטט, על פי רוב קשיחות הדיאפרגמה מתווספת. עם זאת, הפרעות קוואזי-סטטיות עלולות להתרחש מעבר לטווח ההפרעות הקלות, לרוב בטווח של כמה מיקרונים בלבד. במקרה זה, הדיאפרגמה מתגלגלת ואינה מספקת קשיחות נוספת. ליתר בטחון, יש להשמיט את קשיחות הדיאפרגמה מהחישוב ע”י היציבות הסטטית.
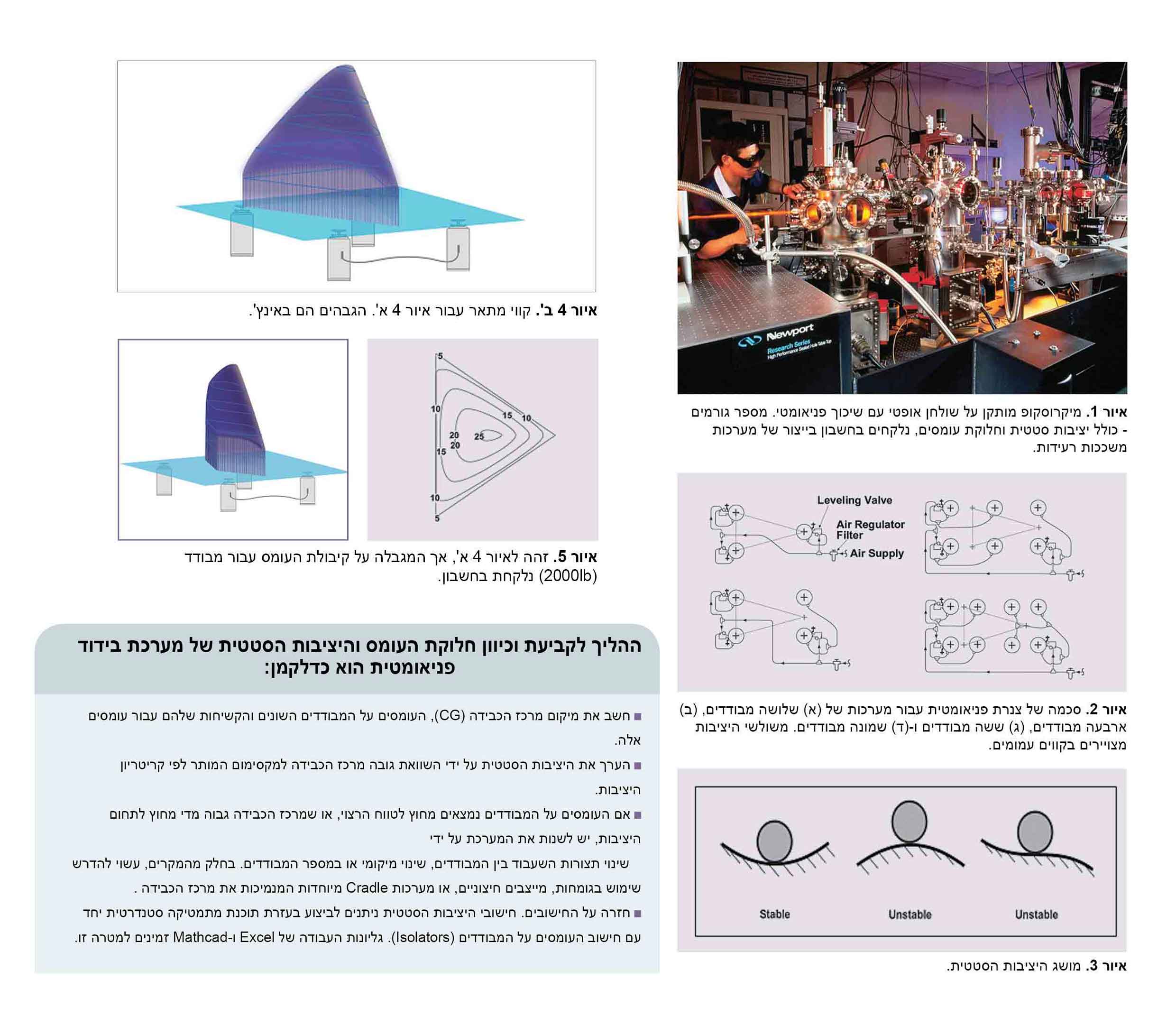
לניתוח היציבות הסטטית, יש לקחת בחשבון סטיה קלה משיווי המשקל המתואר וסיבוב קטן סביב ציר אופקי שרירותי, ולגזור את השינוי באנרגיה הפוטנציאלית, שהוא סכום השינוי (השלילי) באנרגיית הכבידה והשינוי (החיובי) באנרגיה האלסטית הצבורה במבודדים. תוספת אנרגיה פוטנציאלית מובעת בתבנית ריבועית של שתי זוויות סיבוב קטנות סביב שני צירים ניצבים. תבנית זו צריכה להיות חיובית, מה שמוביל לקריטריון יציבות. קריטריון זה קובע את הגובה המרבי המותר של מרכז הכבידה כפונקציה של מיקומו במישור האופקי. פיזית, ישנם שני צירי סיבוב עיקריים עבור כל מיקום של מרכז הכבידה במישור האופקי: אחד עבור הקשיחות הסיבובית המירבית, והשני עבור הקשיחות הסיבובית המזערית.
יציבות דורשת שאף עבור הקשיחות הסיבובית המזערית, העליה באנרגיה האלסטית צריכה להיות גדולה יותר מהירידה באנרגיה הכבידתית עבור סיבובים קטנים סביב הציר העיקרי המתאים. מכיוון שהמבודדים אינם מתוכננים לעמוד בעומסי מתיחה, מיקום מרכז הכבידה מוגבל במישור האופקי על ידי משולש היציבות. תחום היציבות עבור מרכז הכבידה שנובע מכך הוא שטח בצורת כיפה על גבי משולש היציבות, שניתן לתיאור ויזואלי כ-“צלב” של צורות פרבולה ופירמידה. הוא מגיע גבוה יותר עבור מבודדים קשיחים יותר, ונמוך יותר עבור מבודדים רכים יותר. דוגמה לתחום היציבות עבור תצורת שולחן טיפוסית מוצגת באיור 4.
העומס המירבי על כל מבודד הוא מוגבל, ופירושו של דבר הוא שמרכז הכבידה של המערכת כולה צריכה להשאר קרוב למרכז השולחן במישור האופקי. איור 5 מציג את תחום היציבות המופחת, בהשוואה לאיור 4, על ידי הגבלת העומס המירבי על כל מבודד.
שסתומי ישור יכולים להוסיף קשיחות ולשפר את היציבות הסטטית, אך השפעה זו קטנה על פי רוב ולא נחוצה לעיצוב בטוח. מנגד, מערכת הישור העצמי מספקת מנגנון היזון חוזר שיכול להוביל לחוסר יציבות דינאמית. תופעה זו מוגדרת לפי ההגבר של שסתומי הישור. היא תלויה לא רק במיקומים היחסיים של המבודדים ומרכז הכבידה של המערכת, אלא גם בהתפלגות המסה (מומנטים של אינרציה) של המטען. אם היציבות הסטטית של המערכת שולית בלבד, יש לסגור את השסתומים או לסגור אותם כמעט על מנת לשמור על היציבות.
ד”ר ויאצ’סלאב מ.”סלאבה” ריאבוי הוא מהנדס מכני ראשי בתאגיד Newport Corp. ב-Irvine שבקליפורניה.
הכתבה נמסרה באדיבות חברת ניו טכנולוג’י