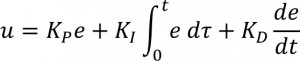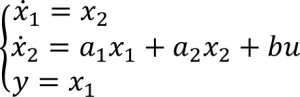ישומי בקרת תנועה נפוצים מאוד כמעט בכל מגזרי התעשייה: אוטמצית מפעלים, רובוטיקה, הרכבה, יצור, בדיקה ועוד. בישומים אלה נדרשת בקרת תנועות מכניות ע”י שליטה על מיקום, מהירות ותאוצה וכן תיאום ושילוב תנועות של מספר רב של צירים או חלקי מכונה. בדומה ליישומים תעשייתיים אחרים, שיטת הבקרה הנפוצה ביותר במקרים אלה היא בקר ה- PID
בקר ה- PID הקלאסי
בקר ה- PID מהווה שיקלול של שלשה מרכיבים:
P – פרופורציונלי תיקון פרופורציונאלי לשגיאת העקיבה הנוכחית.
I – אינטגרלי תיקון פרופורציונאלי לאינטגרל בזמן על שגיאת העקיבה, אשר מבטיח שגיאת מצב מתמיד אפסית.
D – דיפרנציאלי תיקון פרופורציונאלי לנגזרת בזמן של השגיאה, המוסיף ריסון למערכת ומונע תגובת יתר.
כנראה באיור 1, אות הבקרה מהווה צירוף לינארי של שלושת המרכיבים הללו:
כפי שניתן לראות זהו בקר פשטני למדי. פיתוחו הראשוני נעשה בשנות ה- 20 של המאה הקודמת, והפופלריות שלו גדלה ביחוד אחרי מלחמת העולם השנייה, כתגובה לדרישות המתעצמות של האוטומציה התעשייתית. במשך השנים פותחו מספר וריאנטים של אלגוריתם זה וכן נוספו שיפורים כגון הזנה קידמית (feedforward), רשתות תיקון ומסננים לעיצוב תגובת התדר של החוג. עם זאת, העיקרון הבסיסי נותר כליבה של בקרי תנועה מודרניים עד עצם היום הזה.
מהן הסיבות לפופולריות העצומה של בקר זה? בעיקר היותו פשוט ומעשי. ניתן להשתמש בו במגוון רחב של יישומים, ללא צורך במידע מוקדם על המערכת המבוקרת והדינמיקה שלה.
על פי רב ניתן לאפיין מערכת בקרת תנועה טיפוסית באמצעות מערכת משוואות מצב מסדר שני:
כאשר הינו מיקומו של ציר התנועה הינו מהירותו, u הוא אות הבקרה, המהווה פקודת זרם, ו- y הינו המוצא המבוקר. ניתן לראות בקלות ש- מהווה קבוע קשיחות, מקדם ריסון ו- כאשר הינו קבוע הכח (או המומנט) של מנוע המערכת ו- M המסה (או האינרציה) הנעה הכוללת.
למעשה ניתן להוכיח שעבור מערכות מסוג זה תמיד ניתן למצוא בקלות סט הגברים,
אשר ייצב את המערכת ויניב ביצועים סבירים. דבר זה ניתן לביצוע אנליטי בהינתן מודל המערכת, ע”י מדידה וניתוח תגובת התדר של המערכת, או בשיטה המעשית של ניסוי וטעיה.
פשטות היתר של הכיוון, שהפכה את הבקר לישים מאוד ופופלרי כל כך, היא גם בעוכריו.
לבקר PID שלשה חסרונות בסיסיים:
פעולת הגזירה, ההכרחית ליצוב המערכת, רגישה מאוד לרעש. הדבר מגביל את ההגבר האפשרי ולעיתים קרובות מצריך שימוש במסננים המגדילים את פיגור הפאזה ומקטינים את יציבות המערכת.
פעולת האינטגרל, ההכרחית לאיפוס שגיאת המצב המתמיד, מגדילה את פיגור הפאזה, מקטינה את יציבות המערכת, ועשויה לגרום לבעיות רוויה.
סכום משוקלל של שלשה אברים, למרות פשטותו, אינו בהכרח חוק הבקרה הטוב ביותר המתבסס על ערך השגיאה הנוכחי, ערכיה הקודמים וקצב השינוי שלה.
בשל מגבלות אלה, הבקר הבסיסי והפשוט הזה אינו מסוגל עוד לספק את דרישות הביצועים הגוברות של יישומים דורשניים בעולם התעשייתי המודרני. לפיכך מתבצע חיפוש מתמיד של מנגנוני בקרה יעילים יותר שיתנו מענה לדרישות, אך עם זאת ישארו פשוטים ומעשיים.
שיטות בקרה מודרניות
שיטות בקרה מודרניות יותר, כמו ניתוח משוואות מצב, ללא ספק תרמו להבנה מעמיקה יותר של מערכות בקרה בכלל ובקרת תנועה בפרט, למשל בנושאים כמו קונטרולביליות, אובזרווביליות, משערכי מצב (state observer) ומסנני קלמן (Kalman filter).
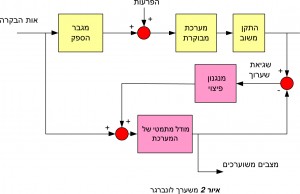
אחד המשערכים המקובלים במערכות בקרת תנועה, הוא “משערך לונברגר”, (Luenberger Observer) שמבנהו הבסיסי נראה באיור 2.
במבנה זה אות הבקרה, שעשוי להיות מוצא של בקר PID רגיל, מוזן למגבר ההספק של המערכת, אך במקביל גם ככניסה למודל מתמטי שלה. המודל המתמטי משמש לשערוך מצבי המערכת, כגון מיקום, מהירות ותאוצה. האותות המתקבלים עשויים להיות איכותיים יותר ופחות רועשים מאלה המתקבלים ממשוב המערכת ומנגזרותיו. מנגנון פיצוי מספק אות תיקון למודל המתמטי ע”י השוואת השערוך עם מדידות המערכת בפועל.
למרות ההתפתחות המואצת של הבקרה המודרנית, ניתן לראות ששיטות בקרה מודרנית עדיין נדירות ביישומים תעשייתיים, ואינן בהכרח ישימות או מעשיות. הסיבה העקרית לכך הינה ששיטות אלה מבוססות על מודל מתמטי שלאו דווקא זמין. גם אם מודל המערכת ידוע, מערכת הבקרה עשוייה להיות רגישה מאוד לשינויים בפרמטרי המודל, ועל כן לסבול מחוסר רובסטיות.
בקרת ServoBoost
חברת “ACS בקרת תנועה” חיפשה פתרון ישים שיאפשר להנות משני העולמות: מצד אחד לרשת מבקר ה-PID את התכונה שהפכה אותו להצלחה: חוקי בקרה פשוטים המבוססים על שגיאת עקיבה של המערכת, ולא על מודל מורכב שלה. מצד שני להשתמש בכלים של הבקרה המודרנית ובמנגנונים אפקטיביים שלה. כך נולד האלגוריתם המכונה בשם המסחרי ServoBoost. האלגוריתם משערך ומקזז הפרעות במערכת באופן כולל ודינמי. הוא מסוגל לשמור על ביצועי ויציבות המערכת גם בהינתן הפרעות ושינויי פרמטרים, הוא מקזז תדרי תהודה בעייתים וכן תופעות לא ליניאריות כגון חיכוך וגליות בכוח המיוצר ע”י המנוע (cogging).
לאלגוריתם זה היתרונות הבאים:
פתרון ישים ומעשי שהוכיח את עצמו במערכות רבות.
רובוסטי לשינויים במערכת.
לא נדרש מידע מוקדם או מודל מתמטי של המערכת.
לא נעשה שימוש בפעולת גזירה רגילה, אשר מגבירה רעשים.
לא נדרש עוד אלמנט האינטגרציה, על הבעיתיות שבו. למעשה חוק בקרה פשוט כמו בקר PD מספיק לקבלת ביצועי המערכת הנדרשים תוך איפוס שגיאות המצב המתמיד. בזאת האלגוריתם מפשט מאוד את בעיית הבקרה.
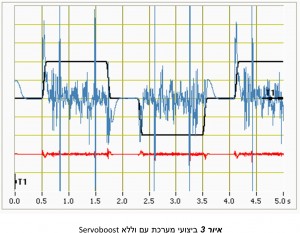
איור 3 מראה דוגמה אופיינית של ביצועי מערכת עם האלגוריתם החדש.
מדובר במערכת לינארית בעלת רזולוציה גבוהה.
הגרף השחור הינו פרופיל המהירות, הגרף הכחול שגיאת העקיבה ללא האלגוריתם, והגרף האדום שגיאת העקיבה תוך שימוש ב- Servoboost. שני הגרפים האחרונים נתונים באותה סקאלה של .
הכתבה נמסרה באדיבות חברת אבירי טכנולוגיות בע”מ