1. הקדמה
בכל מערכת לקליטת אותות רדיו קיים רעש תרמי אקראי המוגדר על ידי “טמפרטורת המערכת” הנקובה במעלות קלווין. חלק מטמפרטורת המערכת נקבע על ידי אנטנת הקליטה ומכונה לכן “טמפטורת האנטנה”. נקדיש את הסקירה הנוכחית להבנת מקורה והשפעתה של טמפרטורת האנטנה.
כל גוף פיזיקלי הנמצא בטמפרטורה כלשהי מעל טמפרטורת האפס המוחלט (0ºK) פולט קרינה אלקטרומגנטית אשר ניתנת לביטוי על ידי טמפרטורת הבהירות (Brightness) Tb. כאשר אנטנת רדיו מכוונת אל גוף כלשהו, הרעש הטבעי שהגוף פולט נכנס לתוך האנטנה דרך האונה הראשית או דרך אונות הצד כמודגם באיור 1. לעיתים קרובות משתמשים במונח “טמפרטורת השמים” כדי לתאר כניסת רעש הנובע מן הסביבה הרחוקה של האנטנה. טמפרטורת הבהירות של עצמים כגון כדור הארץ או הירח, המשוקפת לתוך האנטנה, מקבלת ערכים טיפוסיים שבין 30ºK עד300ºK בתלות בזווית ההטייה של האנטנה ביחס לאופק ובתלות במזג האוויר.
במקרה נדיר יחסית שבו האנטנה מכוונת בדיוק אל השמש, טמפרטורת השמים שלה עשויה להגיע לאלפי מעלות. ארתור ס. קלארק ממציא התקשורת הלווינית חזה אפשרות כזאת ואף חישב את ההסתברות שלווינים “יסונוורו” על ידי השמש. נציין גם את התרומה של טמפרטורת הרקע הקוסמית (3ºK) שמקורה במפץ הגדול והמגיעה באופן אחיד מכל כיוון במרחב.
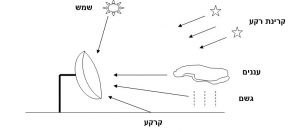
איור 1: טמפרטורות הסביבה הרחוקה הנכנסות לתוך האנטנה
איור 2 [1] מציג את טמפרטורת השמים הנובעת מהפליטה של כדור הארץ עצמו ושל האטמוספירה בתלות בתדר ובזווית הראייה של האנטנה. ניתן לראות כי בתדר 10 GHz אנטנה המסתכלת לכיוון האופק “רואה” טמפרטורת שמים של כ- 100°K ואילו אנטנה המסתכלת לכוון 30 מעלות מעל האופק (מצב סביר בתקשורת לווינים גיאו-סטציונרית) רואה טמפרטורת שמים של כ-20°K.
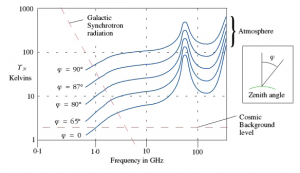
איור 2: טמפרטורת השמים בתלות בתדר ובזווית ההסתכלות קרדיט: [1]
2. חישוב טמפרטורת האנטנה
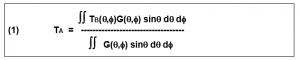
נסמן בעקבות מראי מקום [-42] את טמפרטורת האנטנה הנובעת מטמפרטורת השמים בסימון TA. טמפרטורה זו מציינת את החלק היחסי של הופעת האובייקט בעל טמפרטורת בהירות Tb(θ,Φ) בתוך עקום הקרינה המרחבי של האנטנה G(θ,Φ).
גם האנטנה עצמה מהווה מקור רעש הנובע מן הטמפרטורה הפיזית שלה Tp. נסמן את טמפרטורת הרעש העצמי של האנטנה בסימון Tap הנתונה על ידי
הפרמטר eA מבטא את היעילות התרמית של האנטנה וערכיו הטיפוסיים הם מ-0.8 עד 0.9. ממשוואה (2) רואים שהשפעת הטמפרטורה הפיזית של האנטנה היא קטנה יחסית כאשר eA קרוב ל-1.
הטמפרטורה האפקטיבית בהדקי האנטנה היא אפוא Ta + Tap. טמפרטורה זו עוברת לתוך המקלט דרך קו תמסורת ו/או דרך רכיבים נוספים המייצרים ניחות כלשהו. נסמן את היעילות של העברת הספק הרעש מן האנטנה אל המקלט באות la המבוטאת בערך מוחלט (קטן מ-1). נעיר כי היעילות של העברת ההספק קשורה למונח המוכר יותר של הפסדLa ביחידותdB על ידי הקשרים:
למשל La=0.5 dB מתאים לערך la = 0.9
La = 1 dB מתאים לערך la = 0.8
La = 3 dB מתאים לערך la = 0.5
איור 3 מדגים את המעבר של טמפרטורת האנטנה לתוך המקלט. בהדקי האנטנה הטמפרטורה היא TA + TAP ובהדקי המקלט הטמפרטורה היא Ta
כאשר
Ta טמפרטורת אנטנה בהדקי המקלט
TA טמפרטורת אנטנה הנובעת מטמפרטורת שמים
TAP טמפרטורת אנטנה הנובעת מטמפרטורה פיזית
To = 290ºK טמפרטורת ייחוס
la יעילות העברת הספק הרעש עד המגבר
לבסוף, טמפרטורת האנטנה מתווספת לטמפרטורת הרעש של המקלט עצמו Tr וביחד הן מהוות את טמפרטורת המערכת Tsys
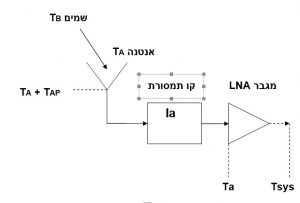
איור 3: טמפרטורת הרעש באנטנה ובמקלט
הרעש הכולל היוצא מן המקלט הוא:
כאשר
k 1.38 x 10-23 [W/°K/Hz] קבוע בולצמן
Tsys טמפרטורת רעש של המקלט במעלות קלווין
B רוחב הסרט במקלט
3. דוגמאות מספריות
- נמצא את טמפרטורת המערכת של תחנת קרקע כאשר טמפרטורת השמים היא TA=20°K. האנטנה נמצאת בטמפרטורת סביבה Tp = 290°K והיעילות התרמית שלה ea = 0.8 לכן TAP = 73°K. נניח la = 0.8 ונקבל בהדקי המקלט Ta = 132°K בהנחה שהמקלט עצמו מוסיף רעש מועט Tr = 75°K (שקול לספרת רעש NF = 1.25 = 1 dB), הרי טמפרטורת המערכת בתחנת הקרקע תהיה Tsys = 207°K.
- נמצא את טמפרטורת המערכת של המקלט הלוויני. כאשר הלווין מכוון לכדור הארץ טמפרטורת השמים שלו היא TA=300°K (טמפרטורת כדור הארץ). האנטנה עשויה להימצא בטמפרטורת סביבה מכסימלית Tp = 320°K והיעילות התרמית שלה היא ea = 0.9 לכן TAP = 36°K. נניח גם כאן כי ההפסד הוא la = 0.8 ונקבל בהדקי המקלט טמפרטורת אנטנהTa = 323°K . בהנחה שהמקלט עצמו מוסיף רעש Tr = 116°K (שקול לספרת רעש NF = 1.4 = 1.5 dB), הרי טמפרטורת המערכת בלווין תהיה Tsys = 439°K.
- אנטנה עם אלומה זוויתית של 5°x0.5° מכוונת בדיוק אל השמש. מהי טמפרטורת האנטנה ? היות והרוחב הזוויתי של השמש הוא בערך 0.5°x0.5° הרי האנטנה “רואה” באלומה הראשית שלה את השמש ולכן טמפרטורת האנטנה קרובה לטמפרטורת השמש, שהיא בערך 6000°K.
4. מבט מערכתי על טמפטורת האנטנה
מובן כי ההשפעה העיקרית של השמים באה לידי ביטוי בתקשורת לווינים או בתקשורת המופנית לחלל. נעיין במשוואת התקשורת הקלאסית על שם Friis
כאשר
Pr הספק נקלט
Pt הספק משודר
Gt שבח האנטנה המשדרת
Gr שבח האנטנה הקולטת
λ אורך הגל
R המרחק בין המקלט והמשדר
נזכיר כי שבח אנטנה G מתקבל על ידי:
כאשר
Aeff השטח האפקטיבי של האנטנה
η נצילות האנטנה (בצלחות היא בדרך כלל 0.6)
בתקשורת לווינים מקובל לנסח את המשוואה בצורה שונה במקצת. הגורם המרכזי שאותו מעוניינים להשיג הוא C/N (Carrier to Noise Ratio) שמשמעותו דומה במידה רבה ליחס אות לרעש S/N . הרעש התרמי במקלט נתון במשוואה (7) לעיל. בתקשורת לווינים נרצה לבודד אתC/N כלומר לקבל את היחס בין הספק הקליטה לבין הרעש התרמי. יחס זה קשור ישירות לרמת השגיאות הצפויה בערוץ. נרשום אפוא את משוואת הערוץ באופן הבא.
כאשר
Pt Gt EIRP = Effective Isotropic Radiated Power
λ²/(4π)² R² הפסד התפשטות גיאומטרי
L הפסד אטמוספרי
Gr/T שבח אנטנת הקליטה חלקי הטמפרטורה
אנו רואים אפוא חלוקה קומפקטית של משוואת הערוץ לשלושה מרכיבים:
EIRP = Pt Gt מרכיב השידור
λ²/(4πR)²L הפסדי המעבר בתווך
(Gr/T) / kBF מרכיב הקליטה
בנקודה זו נעבור לסקלה לוגריתמית של דציבלים, המוגדרת לפי
המאפשרת לעבור מכפל וחילוק לחיבור וחיסור
אנו רואים אפוא כי בערוץ תקשורת המכוון לשמים, נוכח פרמטר קריטי של Gr/T המבטא את רגישות הקליטה וקושר את שבח האנטנה הקולטת עם טמפרטורת האנטנה הקולטת.
5. מבט אל השמש
נציין שלושה נתונים אסטרונומיים ידועים:
מרחק השמש מכדור הארץ R = 1.5 x 1011m
מסת כדור הארץ M = 6 x 1024 kg
קבוע הכבידה העולמי G = 6.6 x 10-11 m3/kg sec2
בהביטנו אל השמש אנחנו מבחינים שניתן לכסות אותה בעזרת קצה האגודל שלנו כאשר היד מושטת למלוא אורכה. מכאן ניתן להעריך את רדיוס השמש כדלקמן: קוטר קצה האגודל 1 cm. מרחק האגודל מן העין1 m לכן זוית הפתיחה היא בערך α = 1/100 rd = 0.5°
נחשב את קוטר השמש: קוטר השמש חלקי המרחק אל השמש שווה לזווית a, כלומר D/R = 1/100 מכאן הקוטר D = αR = 1.5 x 109 m והרדיוס r = 0.7 x 109 m. נמצא גם כי נפח השמש V = (4/3)πr3 = 1.4 x 1027 m3
את מסת השמש נמצא משיווי המשקל בין כוח הכבידה והכוח הצנטרופטלי של הארץ
mω²R = GMm/R² או ω²R = GM/R²
המהירות הזוויתית של כדור הארץ w = 2πf = 2π/T, כאשר מחזור הסיבוב הוא שנה T = 365 x 24 x 3600 sec = 3.2 x 107 sec ולכן M = ω²R3/G = 2 x 1030 kg
צפיפות השמש המתקבלת
ρ = M/V = 2 x 1030 / 1.4 x 1027 = 1.4 x 103 kg/m3 = 1.4 g/cm3
שטף הקרינה המכסימלי של השמש, במרחק R מן השמש (המרחק של כדור הארץ) הוא 1400 W/m2 כלומר דרך משטח כדורי דמיוני ברדיוס R ישטפו 1400 x (4πR²) = 4 x 1026 W וזהו סך ההספק היוצא מן השמש.
חוק Stefan Bolzmann קובע את הקשר שבין טמפרטורה של גוף שחור לבין שטף הקרינה שהוא פולט J = σT4 W/m2 כאשר קבוע סטפן בולצמן הוא
W/m2K4 σ= 5.6 x 10-8מהי אפוא הטמפרטורה הממוצעת על פני השמש ? השטף היוצא מפני השמש הוא סך הספק מחולק בשטח השמש
J = 4 x 1026 /(4πr2) = 0.7 x 108 W/m2
לפי חוק סטפן בולצמן T4 = J/σ = 0.7 x 108 / 5.6 x 10-8 K4
נמצאנו למדים כי T4 = 0.125 x 1016 K4 ומכאן T = 5900 K
בידוע שחוקרי העת החדשה מצאו שטמפרטורת השמש היא כ-5700°K
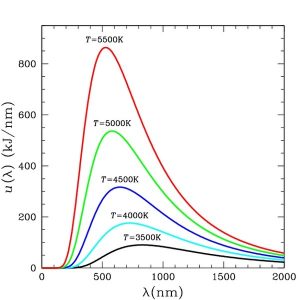
איור 4: ספקטרום הפליטה של גוף שחור בתלות בטמפרטורה שלו קרדיט: [5].
חוק Wien קובע את אורך הגל אשר בו הפליטה מגוף שחור היא מכסימלית, על ידי הקשר λ = 0.003/T [m]. מכאן אורך הגל של הפליטה המכסימלית מן השמש הוא
λ = 0.003 / 5700 m = 0.5m, אך ספקטרום הפליטה מכיל “זנב” ארוך בתדרים רבים

איור 5: מבט טלסקופי על פני השמש קרדיט: Nasa.gov
הפליטה בגלי סנטימטרים היא בערך 7 סדרי גודל נמוכה יותר מן הפליטה האופטית.
וערכה הטיפוסי יהיה 1.4 x 10-4 W/m2 = -70 dBm/m2 . נשים לב לפליטה עודפת בתדרי רדיו כתוצאה מכתמי שמש המסומנת כשמש אקטיבית לעומת שמש שקטה.
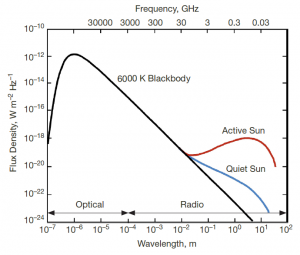
איור 6: עוצמת הפליטה מן השמש בתלות באורך הגל קרדיט: [6].
6. מבט אל המפץ הגדול
באנטנה גדולה,המכוונת לשמים, כך שהבהירות הנצפית קבועה בתחום הזוויתי של אלומת הקרינה, נקלוט הספק רדיו W
W = Aeff B dν [Watt]
B היא הבהירות של הגרם השמימי הנמדדת ביחידות Jansky (Jy)
dν רוחב פס התדרים
Aeff שטח האנטנה
הבהירות הטיפוסית של מקורות רדיו אחדים היא
השמש 107 Jy @ 1 GHz
קסיופיאה A 20 x 10-3 Jy @ 100 MHz
גלקסיית רדיו 20 mJy @ 10 MHz
ענני מימן 1 mJy @ 1420 MHz
פליטת רקע קוסמית 1μJy @ 4 GHz
בשופר המפורסם של מעבדות בל, שבו גילו פנציאס ווילסון את קרינת הרקע הקוסמית, רוחב הסרט היה 10 MHz ושטח האנטנה היה 34 m2 מכאן נוכל לחשב את ההספק שנקלט בשופר.

איור 7: השופר במעבדות בל שבו התגלתה קרינת הרקע הקוסמית קרדיט: Bell Labs 1960
הבהירות B = 1 μJy = 10-32 W/m2Hz
רוחב סרט dν = 10 MHz
שטח האנטנה Aeff = 34 m2
ההספק הנקלט S = Aeff B dν = 3 x 10-24 W
הרעש התרמי N = K T dν
קבוע בולצמן K = 1.38 x 10-23 W/K/Hz
נניח קירור על ידי הליום נוזלי T = 4K
הספק הרעש N = 5 x 10-16 W
שאלה גדולה היא כיצד הצליחו למדוד את אות הרדיו בנוכחות רעש הגדול מן האות ב-8 סדרי גודל ? כדי לקלוט ביחס אות לרעש כה נמוך עלינו להשתמש במסננת LPF ולאחר מכן באינטגרטור (גלאי מעטפת).
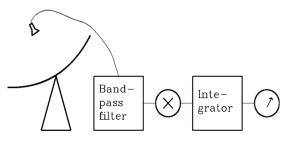
איור 8: סכימת בלוקים של רדיומטר למדידת טמפרטורת מטרה שמימית קרדיט: [7] nrao.
האינטגרטור פועל בזמן t וסוכם N דגימות לפי N = 2 dν
המתח הממוצע ביציאה מוולטמטר הוא V rms = √2 V
בוחרים זמן אינטגרציה ארוך יחסית τ >> 1/dn
טמפרטורת הגלאי Tsys כוללת את כל מרכיבי האות והרעש
שגיאת הטמפרטורה במדידה בודדת σT = √2 Tsys
שגיאת הטמפרטורה של N מדידות σT = √2 Tsys / √N = Tsys / √dν τ
כושר ההפרדה של הגלאי ניתן אפוא על ידי ΔT / Tsys = 1/√dν τ
נניח
dν = 10 MHz
τ = 1 msec
Tsys = 50°K (due to side lobes, clouds etc.)
ΔT = Tsys /100 = 0.5°K
זהו כושר הפרדה מתקבל על הדעת לצורך מדידת טמפרטורת הרקע הקוסמית שערכה הידוע הוא 3°K. רדיומטרים טלסקופים עם זמני אינטגרציה ארוכים ומנגנוני כיול מבוקרים פותחו במצפי הרדיו השונים ברחבי העולם. איור 9 מציג את הרדיומטר המשוכלל במצפה הרדיו GBT[7].

איור 9: גלאי (רדיומטר) מודרני במצפה הרדיו GBT קרדיט: [7].
מראי מקום
[1] Link budget analysis – getting started, p.20, www.RFAtlantic.com
[2] C.A. Balanis, Antenna Theory Analysis and Design, Wiley Inter-science, fourth edition 2016.
[3] Antenna Handbook (editors Y.T.Lo and S.W. Lee), chapter 29: C.H. Liu and D.J. Fang, Propagation, Van Nostrand Reinhold 1988, pp. 29-47 to 29-52.
[4] T. Y. Otoshi, Noise Temperature Theory and Applications for Deep Space Communications Antenna Systems, Artech House, 2008.
[5] M. Majka and T.M. Majka, “Healthy light source”, Researchgate publication 255989402, 2013.
[6] C, Ho, S, Sobin, A, Kantak and S. Asmar, “Solarn Brightness Temperature and Corresponding Antenna Noise Temperature”, IPN Progress report 42-105, November 2008.
[7] www.cv.nrao/course/astr534/radiometers